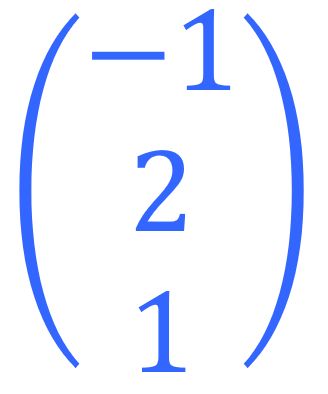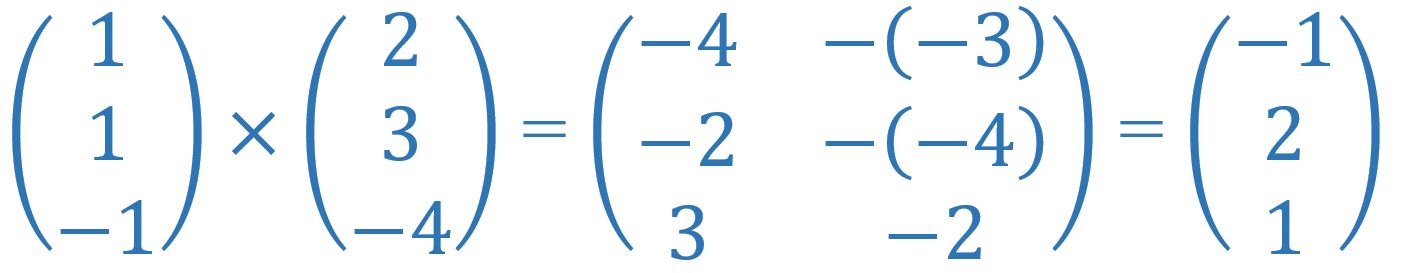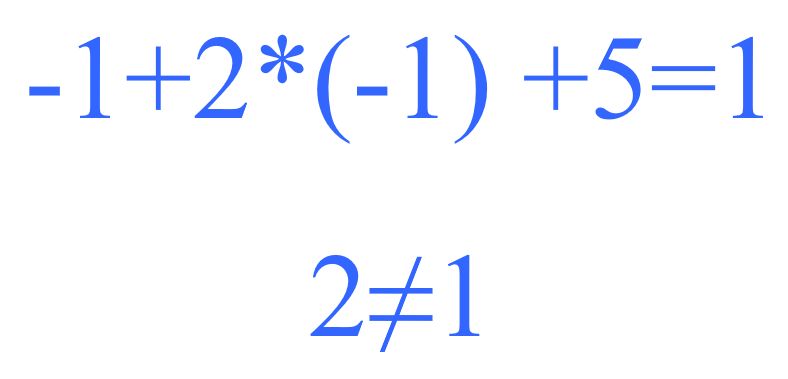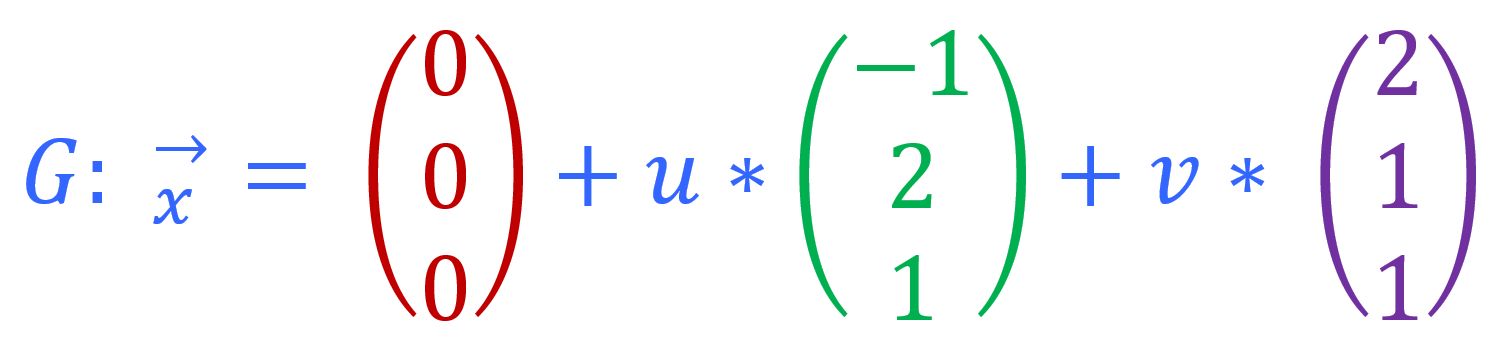Seline Meier - Johanna Espig - Philipp Sakka
Schriftliche Abiturprüfungen
Leistungskursfach Mathematik
Bundesland Sachsen
Schuljahr: 2018/19

-ERSTTERMIN-

Teil A
Lösungen

Lösung 2.1:
Die Funktion f hat bei x=-2 ein Maximum und bei x=2 ein Minimum, somit ist bei diesen Stellen die Steigung gleich Null.
 Die Ableitung der Funktion muss also bei x=-2 und bei x=2 Nullstellen besitzen.
 Damit fällt die Funktion II schonmal weg.
 Eine Tangente der Funktion f hat beim Koordinatenursprung einen Anstieg zwischen 0 und -1. Die Funktion III hat bei x=0 einen y-Wert von y<-1.
Somit ist die Funktion I die Ableitung von f.

Lösung 2.2:
Die Funktion f ist die Ableitung der Stammfunktion F und gibt somit das Monotonieverhalten von F an.
Da die Funktion f im Intervall [1;3] nur negative Funktionswerte hat, ist F in diesem Intervall streng monoton fallend.




Lösung 3.1:

Hierbei muss man einen Punkt finden, sodass die Gleichung des Normalenvektors der Ebene F aufgeht.
Also zum Beispiel der Punkt P(2|1|1) ->  -2+2*1+1=1




Lösung 3.2:
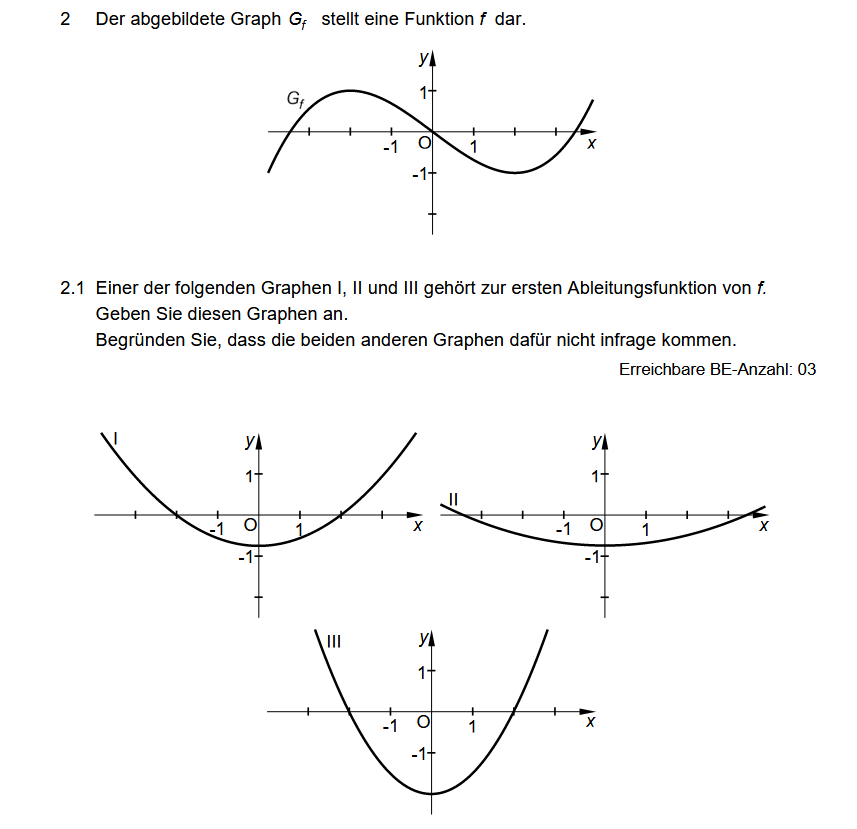
Von F liegt der Normalenvektor vor:

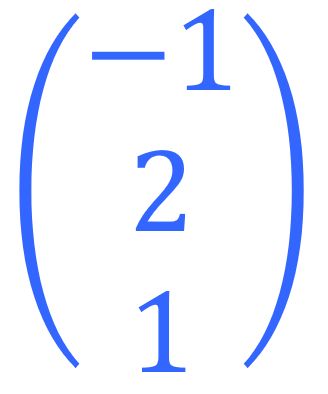Der Normalvektor von E ist:

 
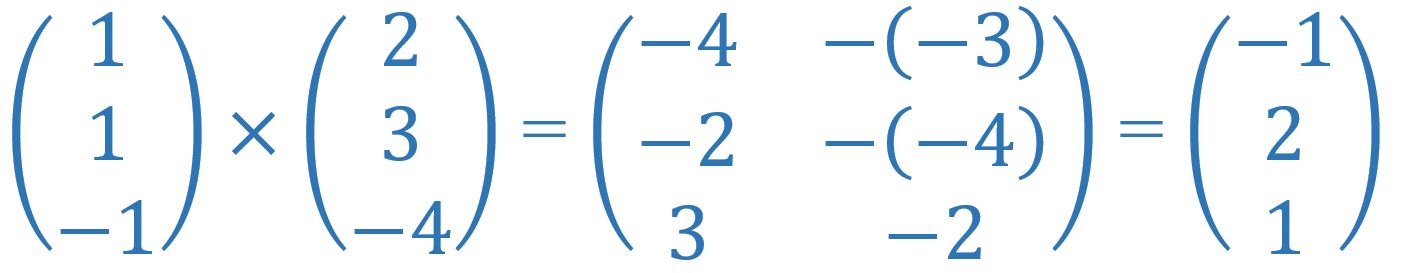
Die Vektoren sind linear abhängig, sie sind also parallel.
Sind sie vielleicht auch identisch?
Punkt von E in Koordinatenform von F einsetzen:

Sie sind nicht identisch.


Lösung 3.3:



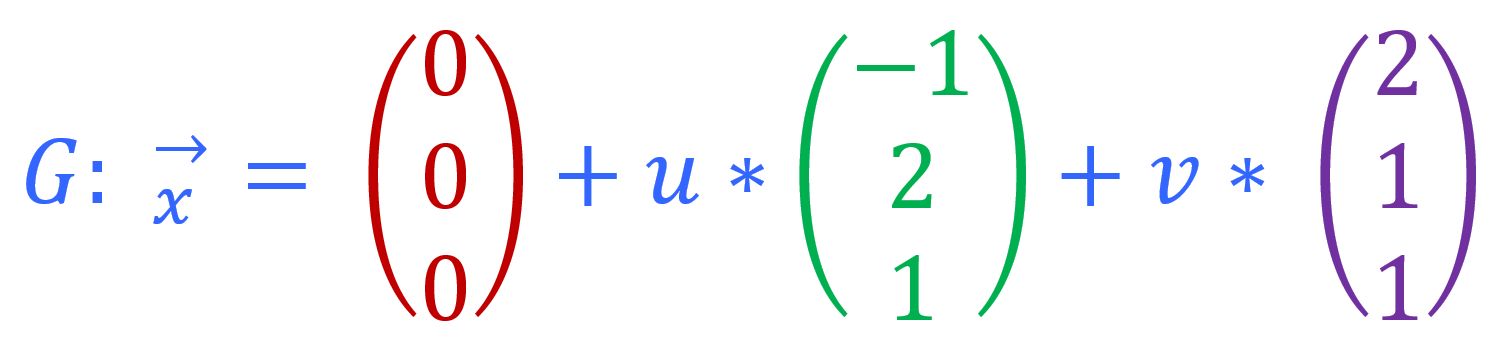
> Koordinatenursprung
> Der Normalvektor von F ist senkrecht zur Ebene, desshalb nehmen wir diesen als Spannvektor.
> Der andere Spannvektor kann ein beliebiger der Ebene F sein, außer der Ortsvektor zum Koordinatenursprung.

zurück zur Startseite